Maximum Profit in Job Scheduling

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You’re given the startTime, endTime and profit arrays, return the maximum profit you can take such that there are no two jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Note: Use iterative approach.

Input Format:

First parameter: integer n, number of jobs.

Second parameter: an integer array startTime, where startTime[i] is the starting time of i^th job.

Third parameter: an integer array endTime, where endTime[i] is the ending time of i^th job.

Fourth parameter: an integer array profit.

Output Format:

Return the number

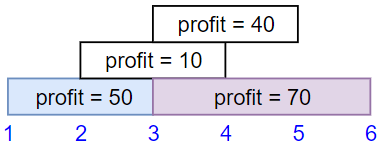
Example 1:

Input:
4
1 2 3 3
3 4 5 6
50 10 40 70
Output: 
120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

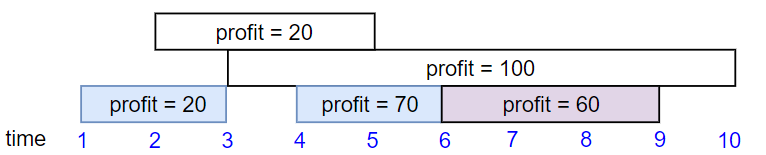
Example 2:

Input:
5
1 2 3 4 6
3 5 10 6 9
20 20 100 70 60
Output: 
150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input:
3
1 1 1
2 3 4
5 6 4
Output: 
6

Constraints:

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 10⁴
• 1 <= startTime[i] < endTime[i] <= 10⁹
• 1 <= profit[i] <= 10⁴
• Time complexity: O(n * log n)
• Auxiliary Space: O(n)